Stanford cs224n 2017 lecture2课堂笔记(1)+ 自己的理解
Reference:
https://web.stanford.edu/class/cs224n/lectures/cs224n-2017-lecture2.pdf
正式开笔前,说说废话,下定决心把Stanford这个系列的课上一遍,好好打打自然语言处理的基础,而又因为纯听课的效果对我而言比不上同时更blog做笔记来得好,因此每日多花些时间来写一写。
Why word2vec?
说到用vector来表达词,一种很常见的方法是离散化的表达,比如one-hot representation, 什么one-hot representation? 假设一个大词库有N个词,想表达Xi, 那么我们就定义一个维度为N的vector,除了第i位为1,其他全为0,举个例子吧:
词库:I have a computer.
每个词的vector为如下形式:
I: [1, 0, 0, 0]
have: [0, 1, 0, 0]
a: [0, 0, 1, 0]
computer: [0, 0, 0, 1]
可是这样离散化表达有什么缺点呢?
- 假设词库很大很大,那么每个词的vector就会很长,后期计算量也会很大,导致我们的模型难以训练;
- 离散化表达难以体现词和词之间的相互关系,比如一个大的词库里,频繁出现“面膜 护肤”等词,按以上的离散化表达,两个one-hot vector向量的dot multiplication(点乘)是0,难以用cosine等方式计算词和词的相似性。
于是~word2vec模型上线,相对于离散化的表达(discrete representation), word2vec模型属于分布式表达(distributional representation),which means “distribution of weights across weight”, 也就是说,区别于长度为整个词库数量N的vector,通常用来表示每个词的vector的维数不会很大,而每个element都有一个数,例如lingusitic: [0.7, 0.3, 0.1, 0.2, 0.5], 这个vector称为词向量,而从单词map到vector这一步,称为word embedding。可见,word2vec通过使用较小维度的vector降低了训练模型需要的space and time complexity,词向量可以通过multiplication(点乘)计算相似性。
两个算法
Skip-grams(SG)
这个算法,是根据给定的词预测词上下文: target -> context
input layer是给定的词,output layer是预测的词上下文,盗了一张参考链接的图:
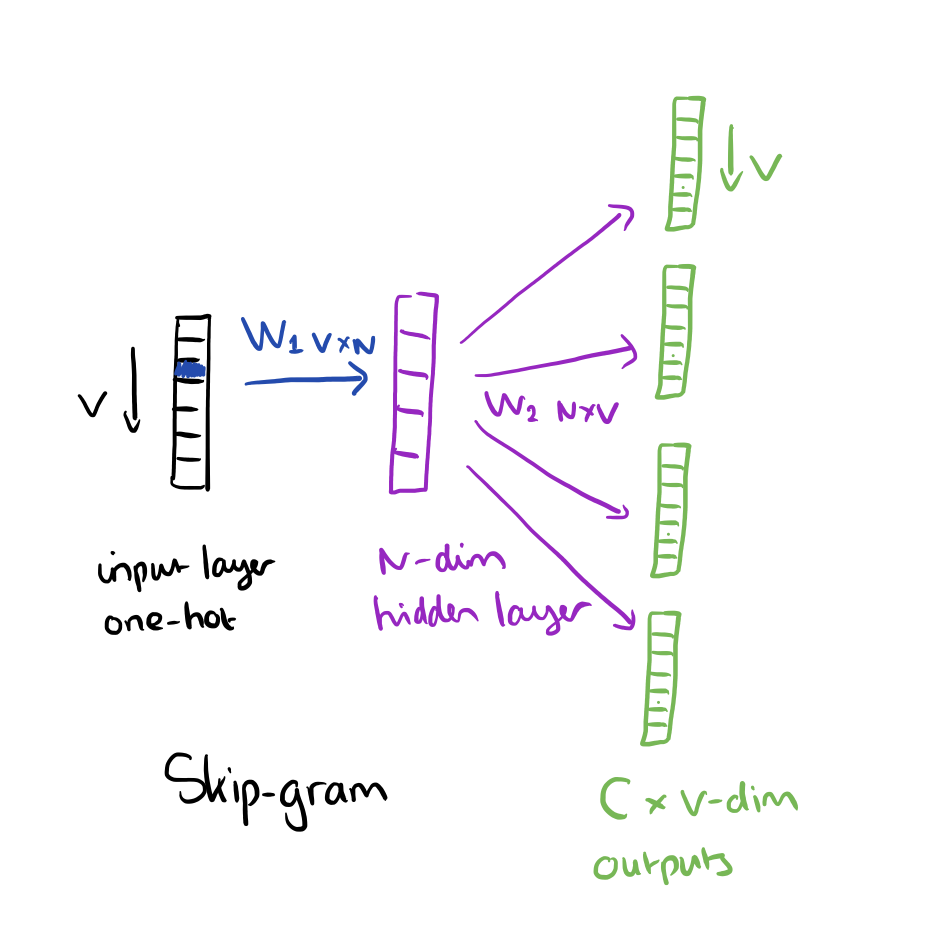
在这个模型里,我们把给定的词用one-hot representation表示,vector的长度V即为词库的词数,从input layer映射到hidden layer,我们需要初始化一个W1(VxN)将one-hot转成词向量,因为one-hot的特殊性质举例:[1, 0, 0, 0],除了特定位置为1,其他位置都为0,因此这个转换词向量的过程,仅仅需要将词向量元素=1的对应的Wmatrix那一行copy就好了,再将hidden layer层乘以W2,得到C个v维词向量,C为word context的词数,每个词向量中,对应位置对高概率的那个词,即为预测词。
Continuous Bag of Words(CBOW)
和skip-gram相反,CBOW根据词上下文环境(word context)来预测这个环境中缺失的那个词,举例
I was born in _, so my native language is Madarine. 这里很明显缺失的那个词为China, 而整个语句为word context,我们的output就是要预测的缺失的词。
再盗图一张,来自相同reference链接。
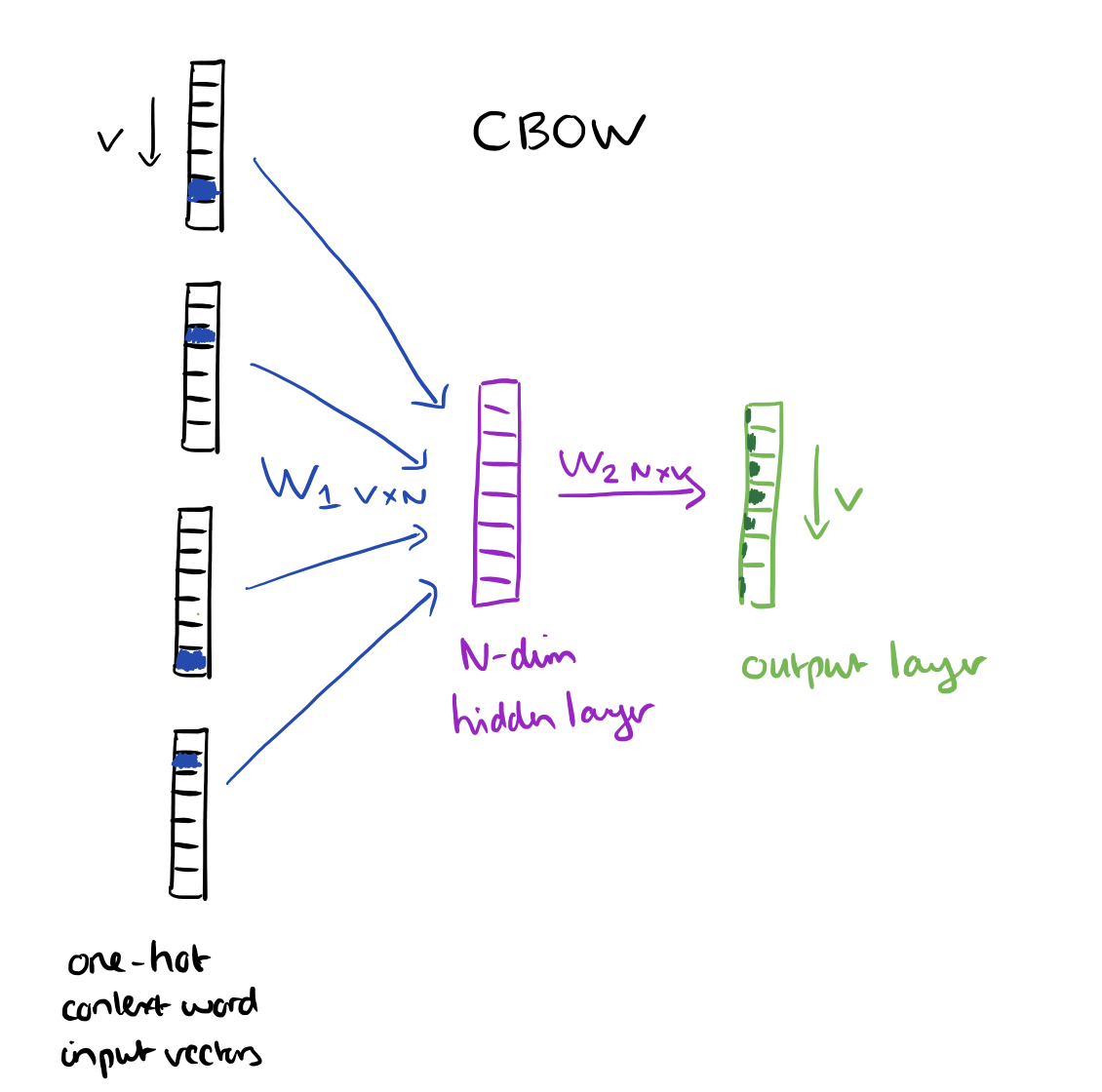
在这个模型中,input layer中输入的是给定word context中所有词(C个)的one-hot vector(V),与weights矩阵W1(VxN)相乘,分别得到多词向量vector(N), 取平均值即为hidden layer,再由hidden layer乘以weights矩阵W2(NxV)得到output词向量v,维度为V,最高分数的那一维度对应的词就是predict word。